Reading Time: 12 minutes

MUSIC & GEOMETRY – PART 1 – INTERVALS & SCALES

In Western music theory there are 13 intervals from Tonic (unison) to Octave. These intervals are the: Unison, Minor Second, Major Second, Minor Third, Major Third, Fourth, Tritone, Fifth, Minor Sixth, Major Sixth, Minor Seventh, Major Seventh and Octave.

Note: click on the interval names for more basic info (Wikipedia). If you are interested in a more esoteric-philosophical perspective on the intervals, then read the article: “The Function of the Intervals” on Roel’s World.

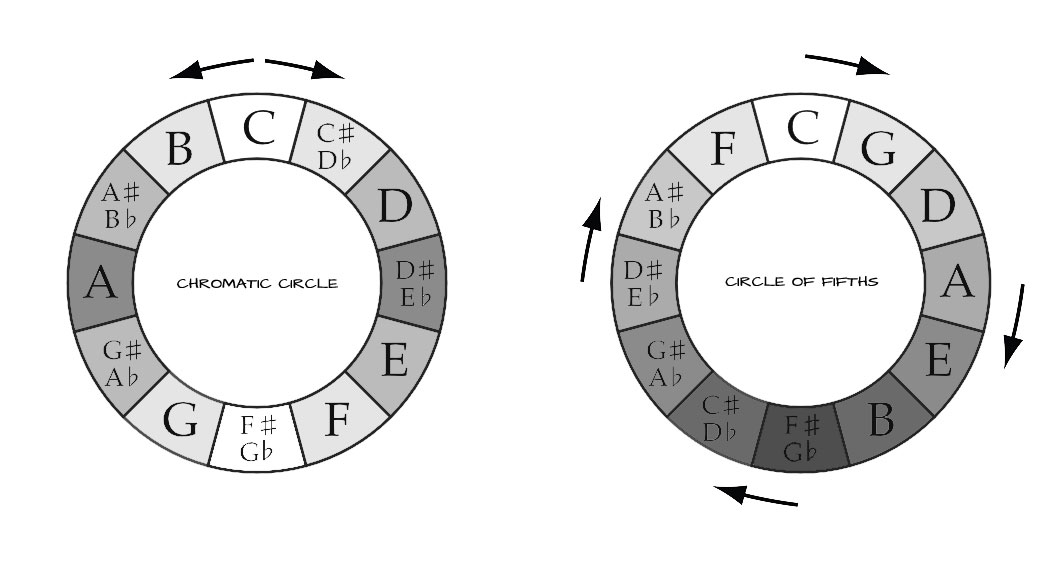
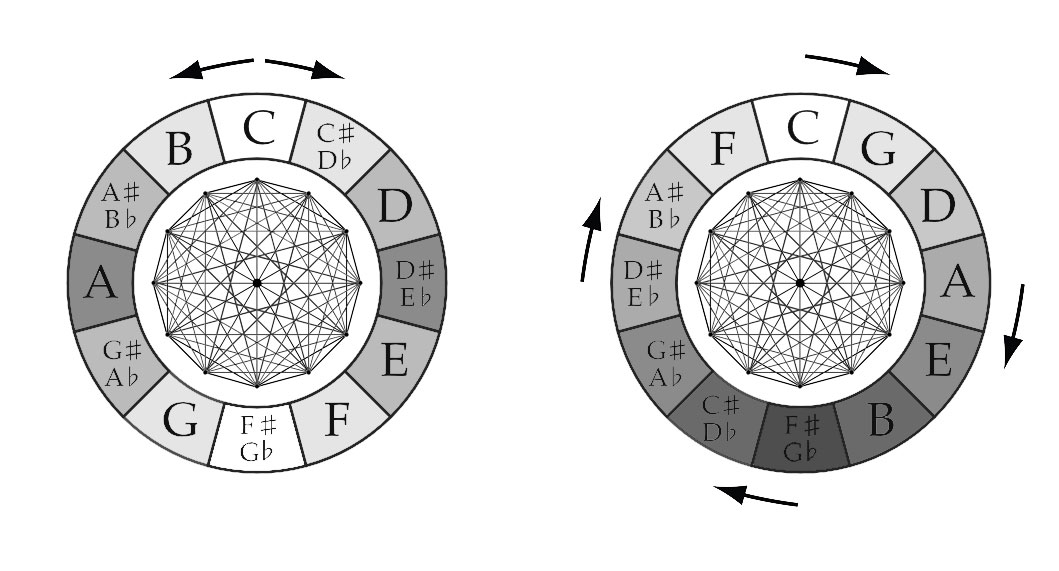
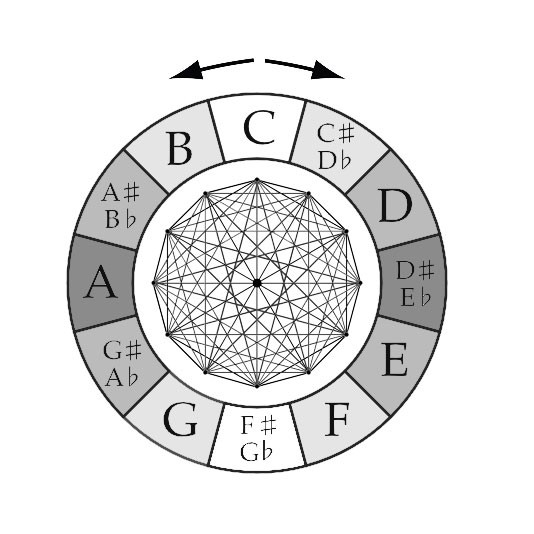
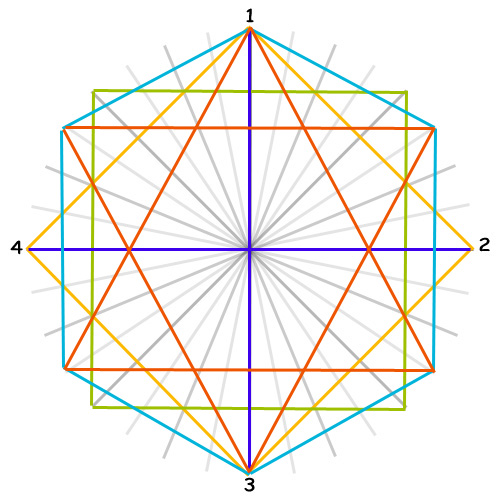
When we look at these intervals and how they relate to one another in the musical tone circles, some geometric shapes appear. The most common tone circles in Western music are the “Chromatic Circle” and the “Circle of Fifths“.

The Chromatic Circle is a visualization of the Chromatic Scale and the 12-Tone Equal Temperament. Both clockwise and counterclockwise movements follow the Chromatic Scale (respectively up and down).

In these articles about music and geometry I have chosen to only us the circles with Major tonalities to have more space for drawing lines between the tones of the circle that form the geometric shapes (polygons and polygrams).

The Circle of Fifths is based on the stacking of (Perfect) Fifths, characteristic for the Pythagorean Temperament. If you move around the circle clockwise you go up a Fifth with every “step” you take, if you move around the circle counterclockwise you go up a Fourth with every “step” you take.

What is important to make note of though, is that the Circle of Fifths (on the right) is geometrically drawn incorrectly. With the Circle of Fifths starting on C going clockwise around, all 12 sections should be drawn a tiny bit bigger. The result of this is that the last section (F) would slide over the first section, but would become smaller then the other 11 sections, if you close the circle (the Wolf Interval). When “Stacking” perfect Fifths the Circle isn’t closed, but creates a spiral, the C after the F slightly overshoots (approx. about the size of a Quartertone.

For perfect geometric shapes, you should always use an “Equal Temperament”. Any “Just Temperament” (based on the Harmonic Series) will not result in perfect geometric shapes.

GEOMETRY OF INTERVALS – ‘CONNECTING THE TONES’

There are many ways to visualize the connection between tones. One of the more “common” methods is to use geometric shapes, at least for the visual oriented persons and/or mathematical minds among us.

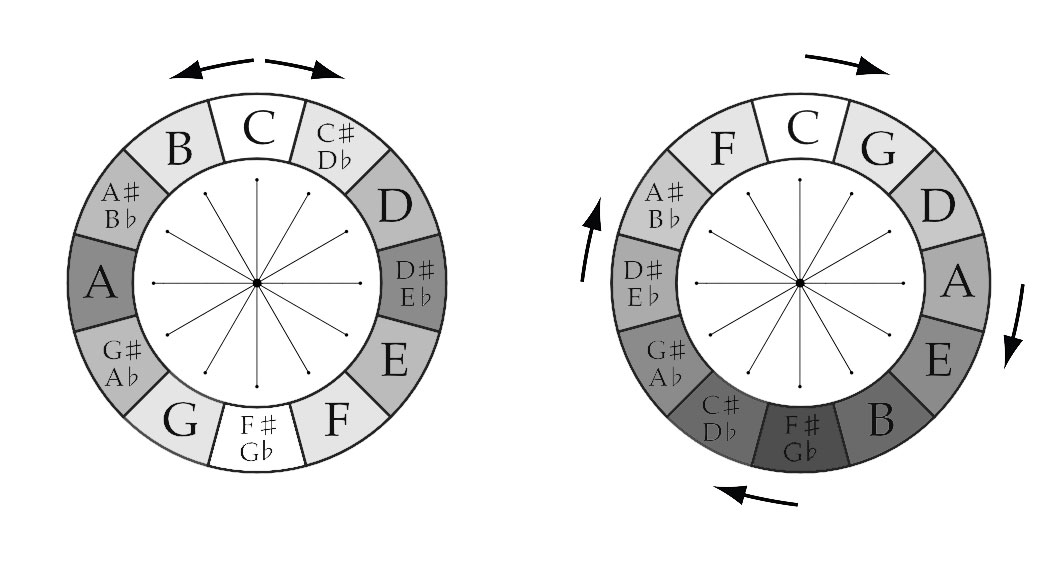
LINE
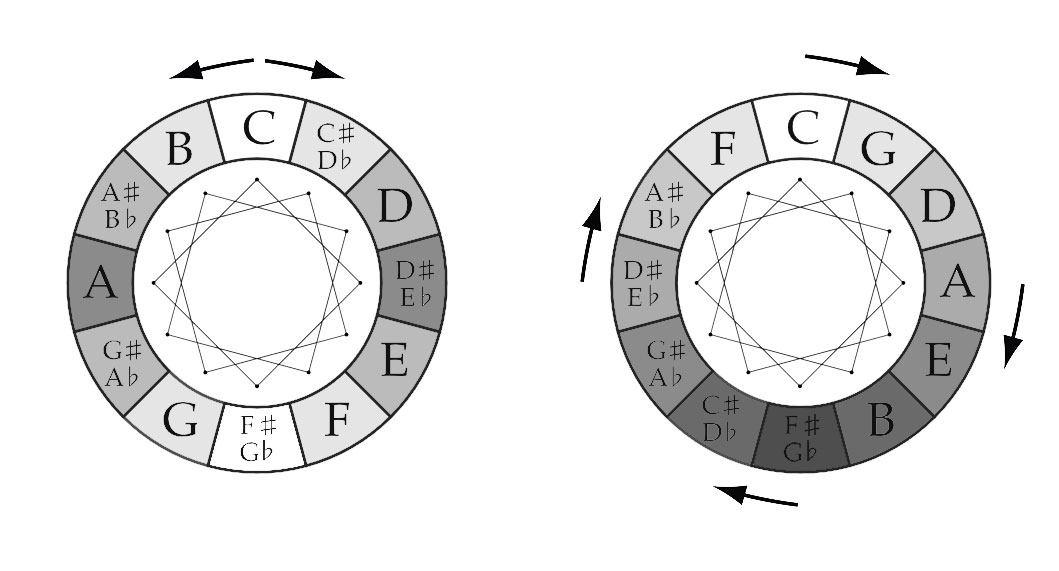
The simplest “shape” is a line. The “connected” tones in the Chromatic Circle and the Circle of Fifths are a “Tritone“ apart from one another: C-G♭, G-D♭, D-A♭, A-E♭, E-B♭ & B-F.The lines drawn represent Equal Tempered Tritones of 600 cents.

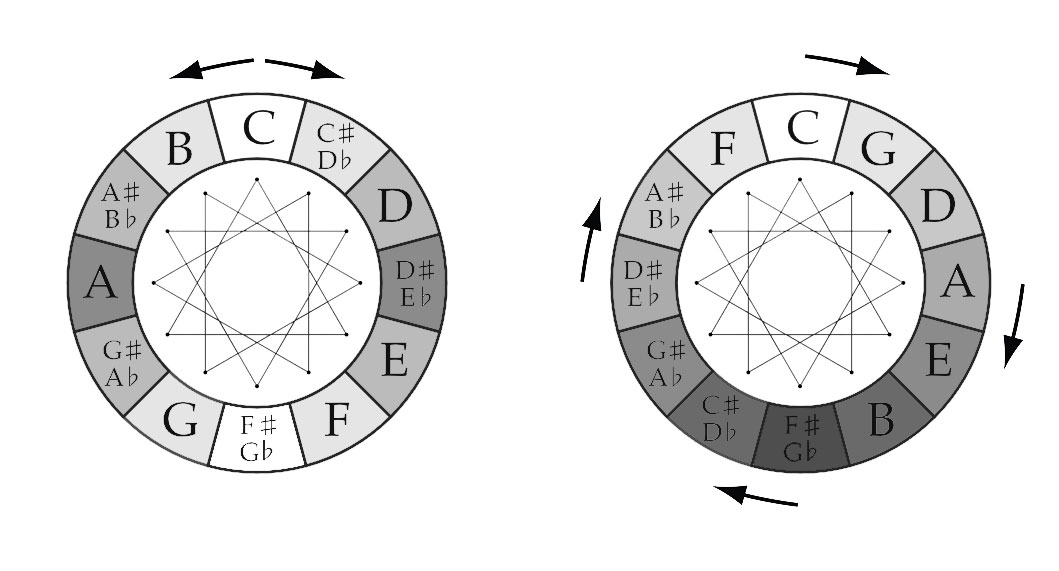
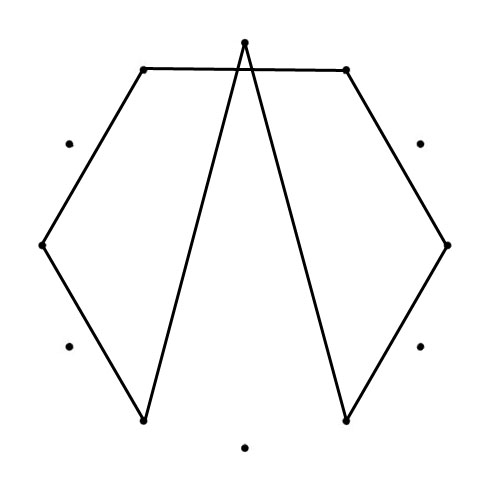
TRIGON (triangle)
The clockwise “connected” tones are a Major Third (400 cents) apart from one another: C-E, E-A♭ & A♭-C / G-B, B-E♭ & E♭-G / D-G♭, G♭-B♭ & B♭-D / A-D♭, D♭-F & F-A. (800 cents) apart.

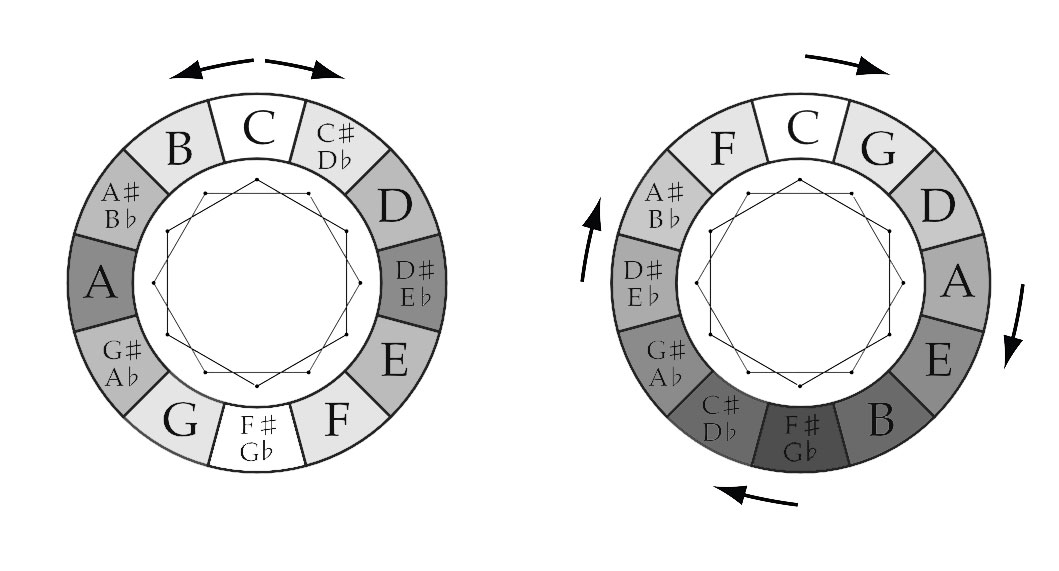
SQUARE
In the Chromatic Circle the clockwise “connected” tones are a Minor Third (300 cents) apart from one another: C-E♭, E♭-G♭, G♭-A & A-C/B♭-D♭, D♭-E, E-G & G-B♭ / F-A♭, A♭-B, B-D & D-F. Counterclockwise (going up the scale) the “connected” tones are a Major Sixth (900 cents) apart.

With the Circle of Fifths you have to swap the direction to get the same interval.

HEXAGON
The “connected” signs form two Hexatonic or Whole Tone Scales when combined: C–D–E–G♭–A♭–B♭–C and B–D♭–E♭–F–G-A-B. The clockwise “connected” tones are a Major Second (Whole Tone, 200 cents) apart, counterclockwise (goung ip the scale) they are a Minor Seventh (1000 cents) apart.

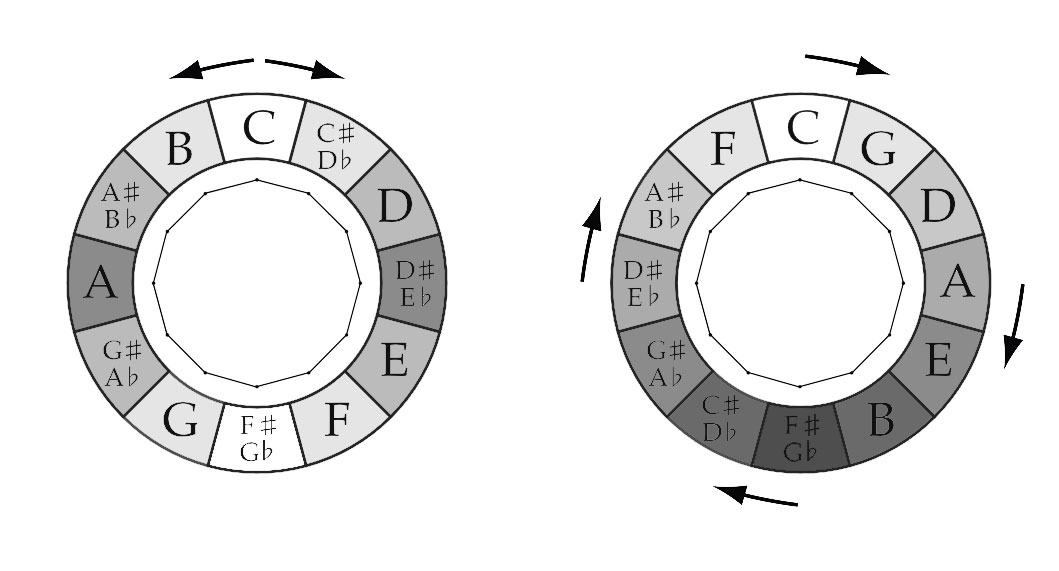
Dodecagon - Fourths & Fifths - Chromatic

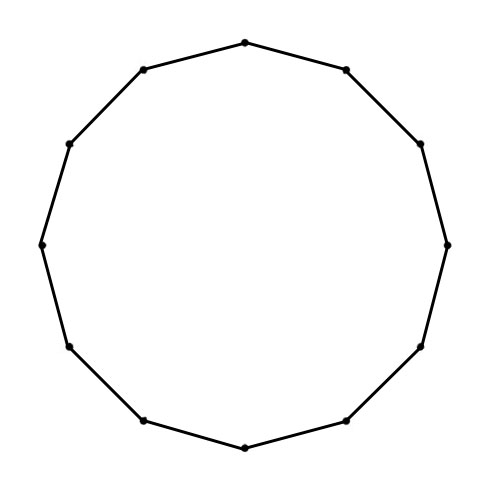
DODECAGON
The Chromatic Circle visualize the Chromatic Scale: clockwise in Minor Second (100 cents) and counterclockwise (going up the scale) Major Seventh (1100 cents). The Circle of Fifths visualizes clockwise the Fifths (Equal Tempered 700 cents), counterclockwise the Fourths (Equal Tempered 500 cents).

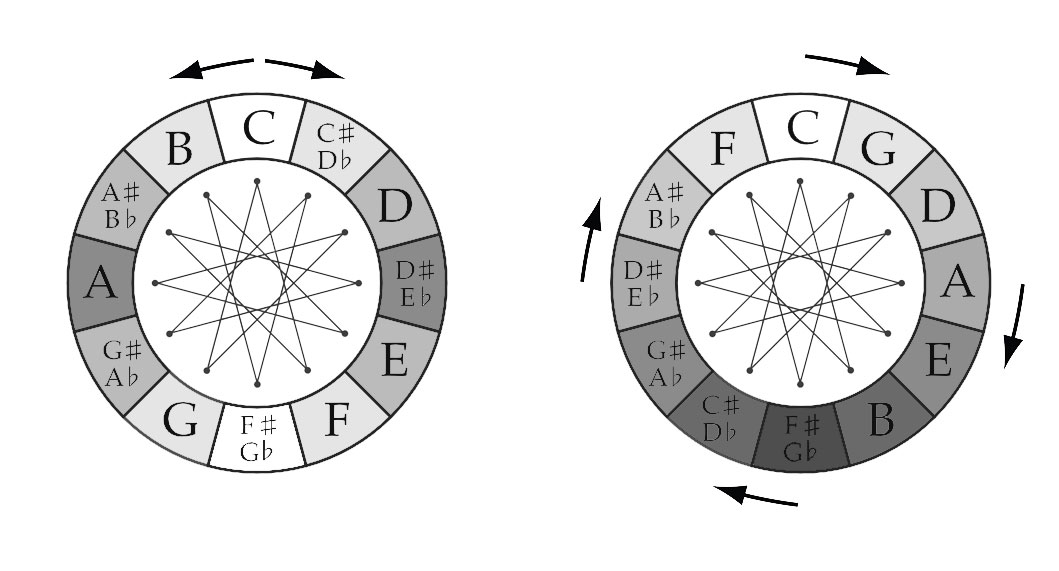
Dodecagram - Fourths & Fifths - Chromatic

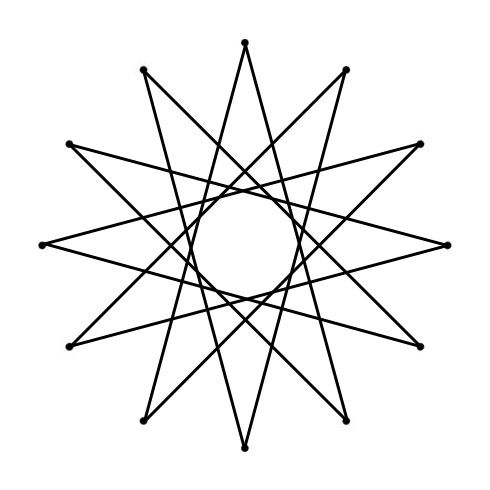
DODECAGRAM
When you follow the lines of the Dodecagram across the Chromatic Circle, you find clockwise the Fifths (700 cents) and counterclockwise the Fourths (500 cents). The Circle of Fifths visualizes the Chromatic Scale: clockwise in Minor Second (Equal Tempered 100 cents) and counterclockwise (going up the scale) Major Seventh (Equal Tempered 1100 cents).

SUPERIMPOSED
With these geometric “shapes” combined, all possible tone-connections (intervals) of the 12-Tone system can be made, as is clear from the combined graph.

NOTE: As I have mentioned earlier, perfect Geometric shapes relate to the 12-Tone Equal Temperament. Just Intonated intervals are larger or smaller then the Equal Tempered ones. This means that the geometric shapes would not “close” (end where they started) or result in shapes that ain’t symmetrical.

When stacking Just Intervals a spiral appears, not a closed tone-circle such as the Chromatic Circle. So, even though Just Intonated intervals are more consonant, sound more natural (Harmonic Series), are more pleasing to the ear, the geometric shapes will be less then perfect. This by itself “proofs” (in my opinion) that a perfect geometric shape or mathematical formula does not per definition generate or represent the most perfect tone/interval/chord/scale/sound.

It is good to note though, that a spiral is considered mathematically symmetrical as well, the combination of a central dilation and a rotation whose centers are distinct is also “spiral symmetry”. Geometrically (visually) though the spiral isn’t symmetrical as the (Equal Tempered) shapes seen in the circles above that have “Reflection” (or “Mirror”) Symmetry, Rotational Symmetry and Point Symmetry.

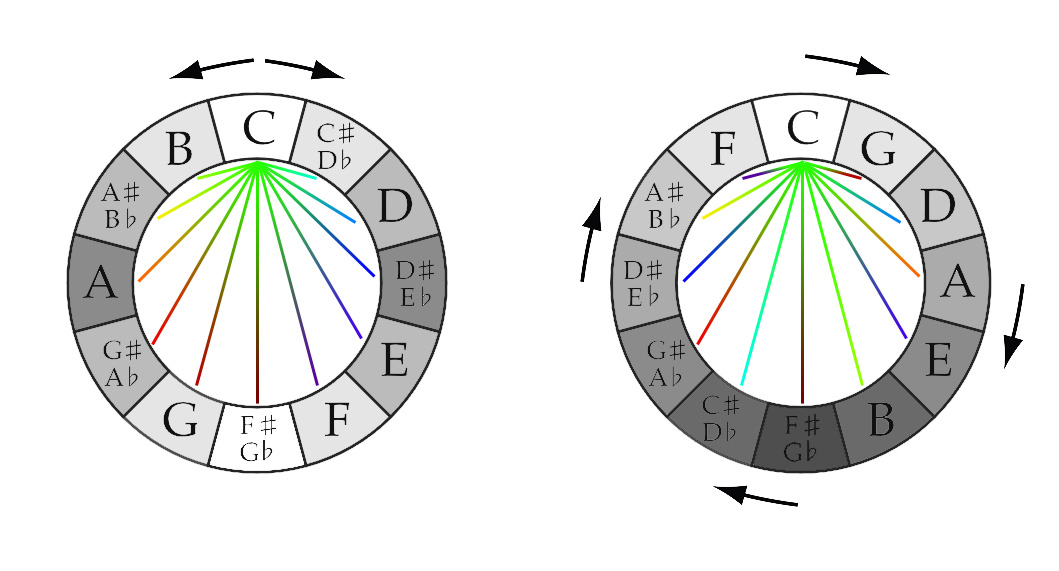
Superimposed - all intervals from tonic C

INTERVALS SUPERIMPOSED FROM ONE TONIC (IN COLOR)
This is what all intervals related to only one tonic (in this example the tone C) would look like. The colors used at the tone-color combination (Concert Pitch 440Hz) as described in the Roel’s World article about Sound (Music) & Light (Color).

THE TETRACTYS & MUSICAL INTERVAL RATIOS

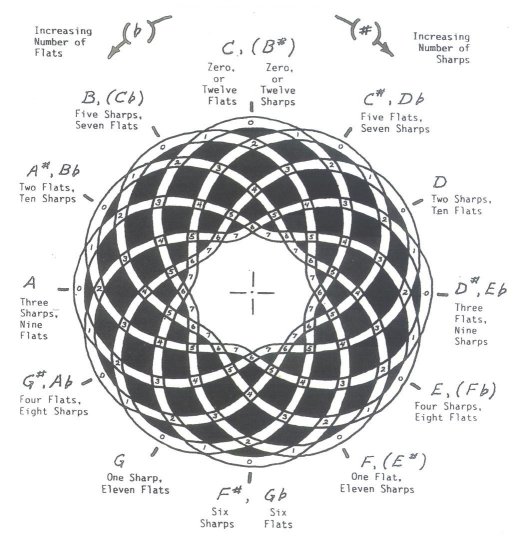
The tetractys (Greek: τετρακτύς), or tetrad, or the tetractys of the decad is a triangular figure consisting of ten points arranged in four rows: one, two, three, and four points in each row, which is the geometrical representation of the fourth triangular number. As a mystical symbol, it was very important to the secret worship of Pythagoreanism.

You can see the Tetractys as a geometric representation of many Just interval ratios (when relating a row to one or more above).

You might have noticed already the Octave 2:1, as well as the Just Fifths (3:2) – the Pythagorean scales are based on the stacking of the Just Fifth – and it’s inversion, the Just Fourth (4:3).

When just looking at the single dot on top, you can “picture” the Tonic or Unison (1:1).

Now, picture the Tetractys to extend beyond the row with 4 dots, with more dots: 5, 6, 7, 8 … et cetera, then we get: 5:4 (Just Major Third), 6:5 (Just Minor Third), 7:6 (Septimal Minor Third), 8:7 (Septimal Major Second), 9:8 (Pythagorean Major Second), 10:9 (Small Just Whole Tone), 11:10 (Neutral Second or “Ptolemy’s Second”), 12:11 (Undecimal Neutral Second), et cetera …

And if you would “skip” a row in the Tetractys, more intervals appear: 3:1 (Just Twelfth), 5:3 (Just Major Sixth), 7:5 (Septimal Tritone), 9:7 (Septimal Major Third), 11:9 (Undecimal Neutral Third), et cetera …

Or “skip” 2 rows and even more intervals appear: 4:1 (Fifteenth or Two Octaves), 7:4 (Harmonic Seventh), 8:5 (Just Minor Sixth), 10:7 (Septimal Tritone), et cetera …

And how about “skipping” 3 rows: 9:5 (Greater Just Minor Seventh), 11:7 (Undecimal Minor Sixth), 15:11 (Undecimal Augmented Fourth / ‘Tritone‘), et cetera …

As you can see, many intervals can be formed by looking at the Tetractys as geometric representation of musical ratios. You can find an extensive list of intervals on Wikipedia where you can find additional ratios that related to the extended Tetractys displayed in this article.

TORUS KNOT TONE CIRCLE

I came across this interesting-looking Tone Cirle in the shape of a torus knot online. It’s a bit different then the other tone-circles shared in this article but it is an interesting (pretty) concept nonetheless, so I’ll share it here.

If we start from C and follow the strand from “0” to “1” to either side and move to “0” outwards again then we have moved a semitone up or down the scale and end up at C♯ or B. Et cetera …

⟲	STEPS ON STRANDS	⟳
Major 7nd	0 ⇠ 1 ⇠ 0 ⇢ 1 ⇢ 0	Minor 2nd
Minor 7nd	0 ⇠ 2 ⇠ 0 ⇢ 2 ⇢ 0	Major 2nd
Major 6th	0 ⇠ 3 ⇠ 0 ⇢ 3 ⇢ 0	Minor 3rd
Minor 6th	0 ⇠ 4 ⇠ 0 ⇢ 4 ⇢ 0	Major 3rd
5th	0 ⇠ 5 ⇠ 0 ⇢ 5 ⇢ 0	4th
Tritone	0 ⇠ 6 ⇠ 0 ⇢ 6 ⇢ 0	Tritone
4th	0 ⇠ 7 ⇠ 0 ⇢ 7 ⇢ 0	5th

NOTE: The information about this “tone knot” provided in the source article in question is wrong! The writer calls this “tone knot” a “Circle of Fifths” instead of a “Chromatic Circle“. Of course one could assign the Circle of Fifths to the Torus Knot as well, but that is not what we see in the image provided. The writer also calls the Fourths and Fifths “Major“, but Fifths and Fourths are neither Major nor minor.

GEOMETRY OF SCALES

A scale is a serie of tones at specific distances (intervals) from each other. The most common tone distances used in scales are semitones (“s” or “h” = half tone) and tones (“T” or “W” = whole tone / 2 semitones), but some scales do include larger intervals like the minor third (m3 = 3 semitones) and Major third (M3 = 4 semitones).

There are many different scales, too many to list them all in this article. Most scales (including the most common Major and Minor scales) are asymmetrical, only a small number of scales are symmetrical. I will only list a few of the most used scales, as well as several (less often used but) symmetrical scales.

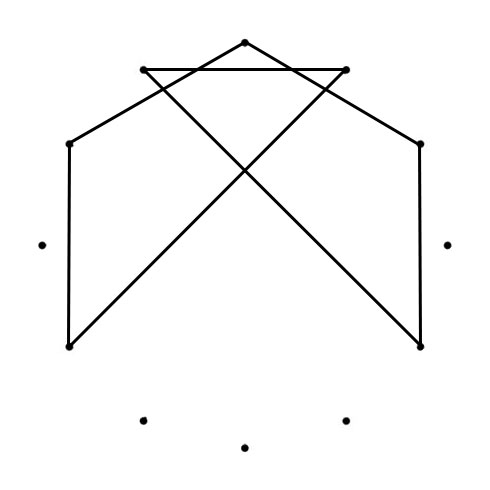
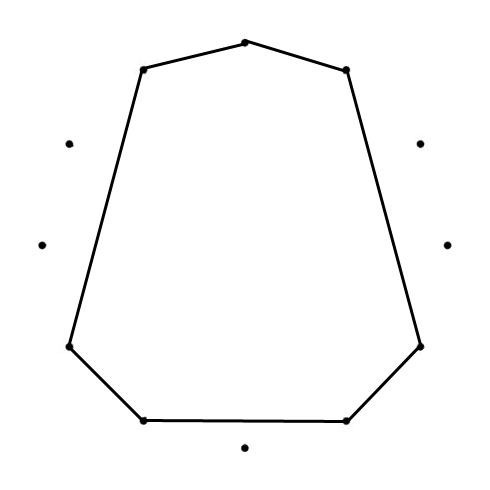
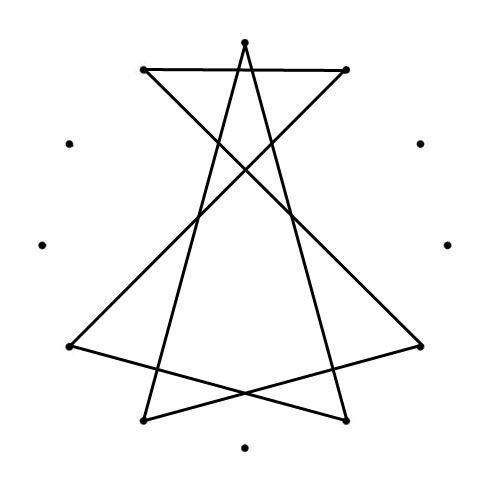
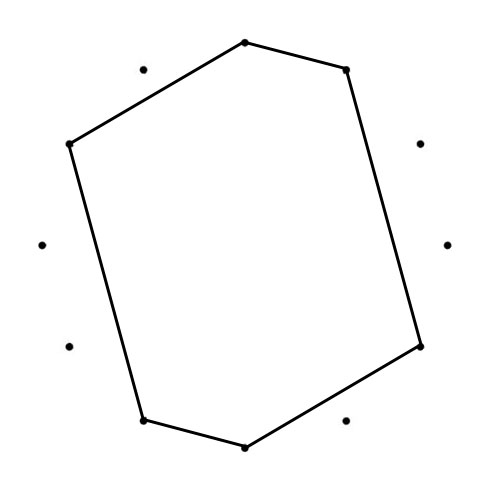
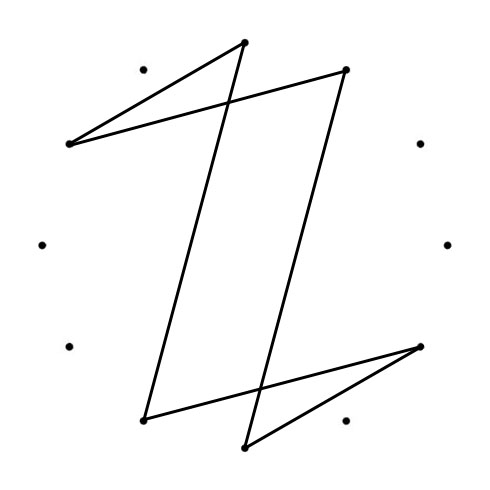
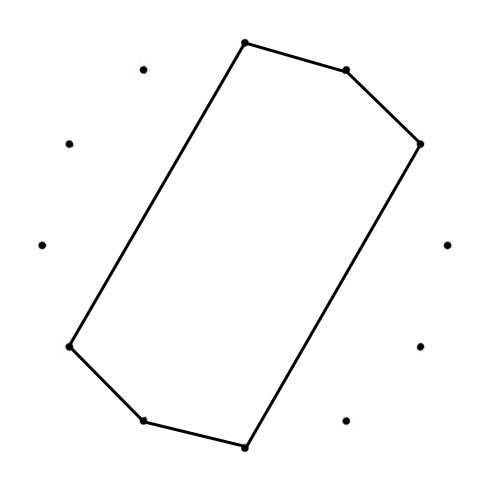
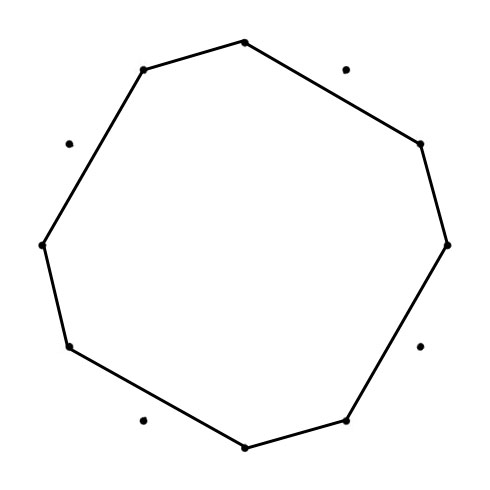
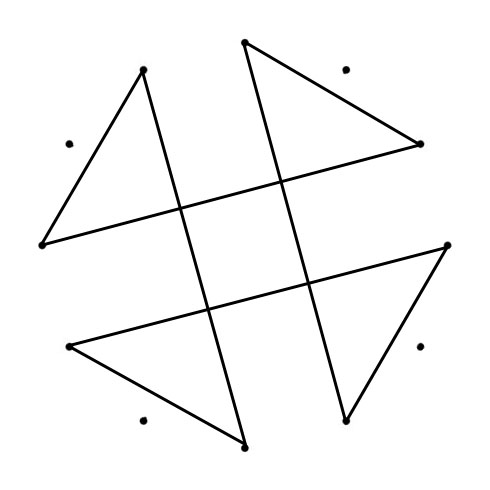
C MAJOR AND C NATURAL MINOR SCALES

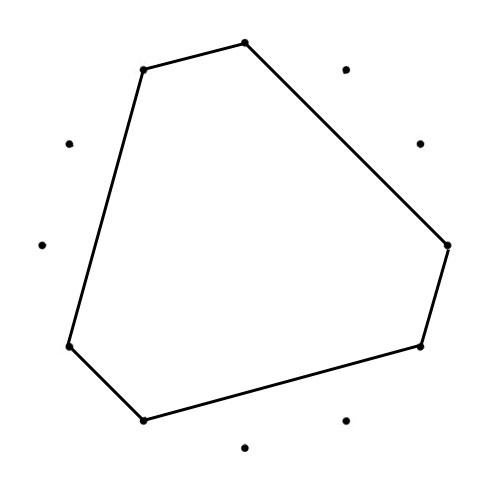
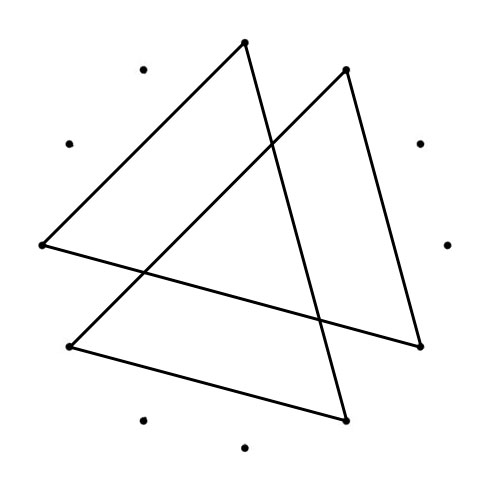
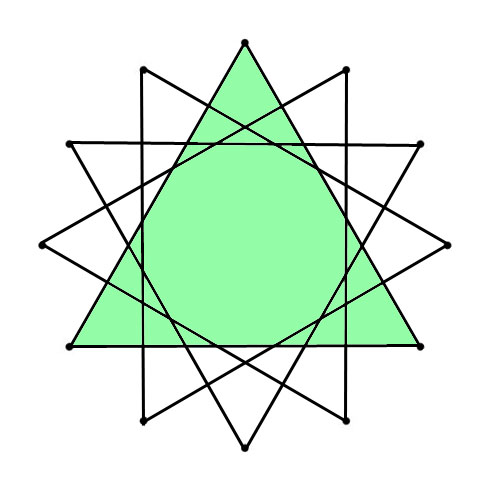
When you connect the tones of scales (in sequence), Polygons (with Chromatic Circle) and Polygrams (with Circle of Fifths) appear. With all scales below the tone “C” is represented by the dot on the top):

The Major and Minor polygons (or “Greek Modes Polygram) drawn in the Chromatic Circle (CC) are the same shape just tuned, from Major to Minor with 90 degrees clockwise (CC). The Major and Minor polygrams drawn in the Circle of Fifths (CoF) are turned (Major to Minor) with 90 degrees counterlockwise (CoF). Another interesting thing happens when you superimpose both polygons. You can place a “Mirror” where one half of the superimposed shape mirrors the other half.

Every first image bellow visualizes the Chromatic Circle (CC), every second the Circle of Fifths (CoF).

C MAJOR (IONIAN)

T–T–s–T–T–T–s

W–W–h–W–W–W–h

2-2-1-2-2-2-1

C MINOR (AEOLIAN)

T–s–T–T–s–T–T

W–h–W–W–h–W–W

2-1-2-2-1-2-2

C MAJOR & MINOR

SUPER-
IMPOSED

MIRRORED

The two tones of the circles are not part of the superimposed C Minor and C Major polygons / polygrams are the C♯/D♭ and F♯/G♭. In both scales the intervals formed between those tones and the tonic (C in this case) – respectively a Minor Second and Tritone – are considered the most “dissonant” intervals in the scale.

GEOMETRY OF THE GREEK MODES

All “Greek Modes” use the same shape polygon as the Major and Minor scales (Chromatic Circle). On the left an image of the IONIAN mode (or Major scale) polygon (with the tone C on top). The polygons of the other Greek Modes can be found by simply rotating the polygon:

the DORIAN mode polygon is rotated 60 degrees (2 semitones) counterclockwise.
the PHRYGIAN mode polygon is rotated 120 degrees (4 semitones) counterclockwise.
the LYDIAN mode polygon is rotated 150 degrees (5 semitones) counterclockwise.
the MIXOLYDIAN mode polygon is rotated 150 degrees (5 semitones) clockwise.
the AEOLIAN (Minor) mode polygon is rotated 90 degrees (3 semitones) clockwise.
the LOCRIAN mode polygon is rotated 30 degrees (1 semitone) clockwise.

You can also say the sequence of Whole (W) and Half (h) tones is “shifting”:

W – W – h – W – W – W – h = Ionian (the Major scale)
W – h – W – W – W – h – W = Dorian
h – W – W – W – h – W – W = Phrygian
W – W – W – h – W – W – h = Lydian
W – W – h – W – W – h – W = Mixolydian
W – h – W – W – h – W – W = Aeolian (the Minor scale)
h – W – W – h – W – W – W = Locrian

The fat W in the list above is the Whole Tone distance between the G and A in the polygon, opposite the D.

The shape of the “Greek Modes Polygon” might look a bit “odd” at first. This changes though, when you turn the Chromatic Circle and the Ionian Mode polygram itself 60 degrees counterclockwise:

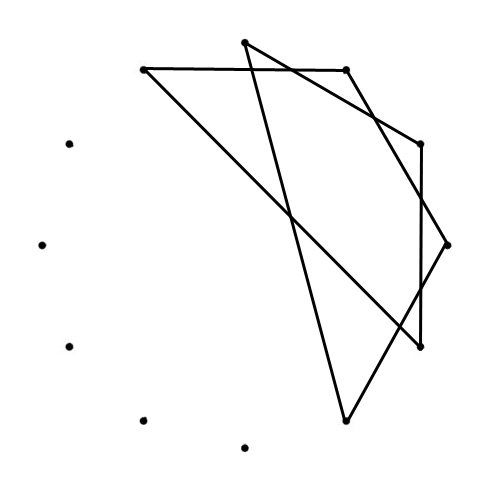
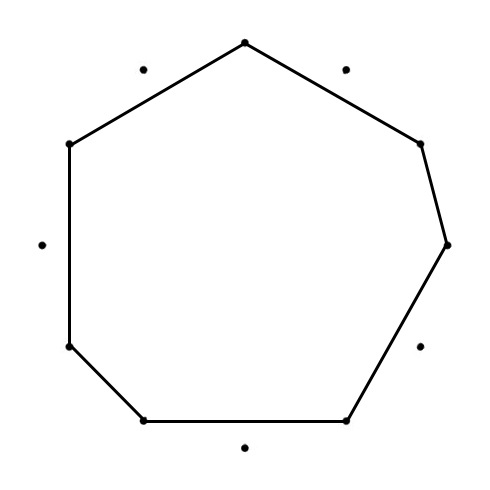
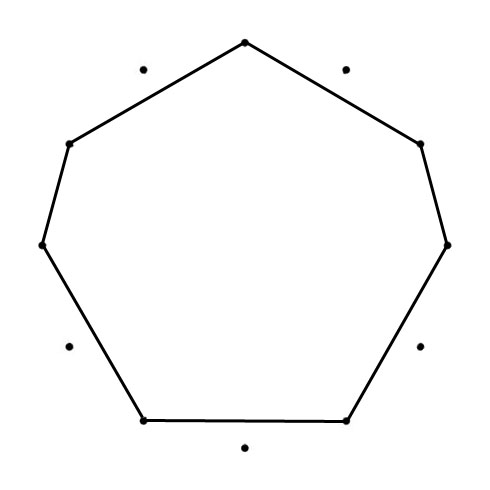
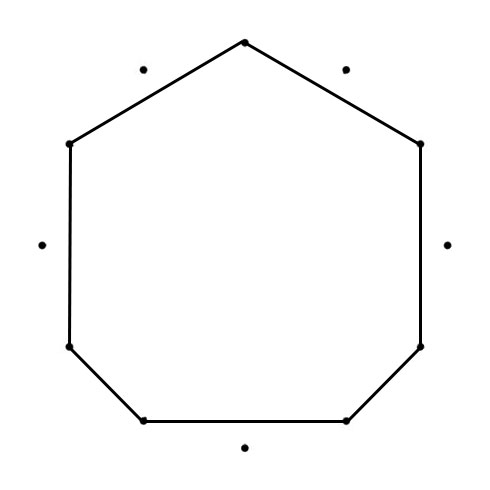
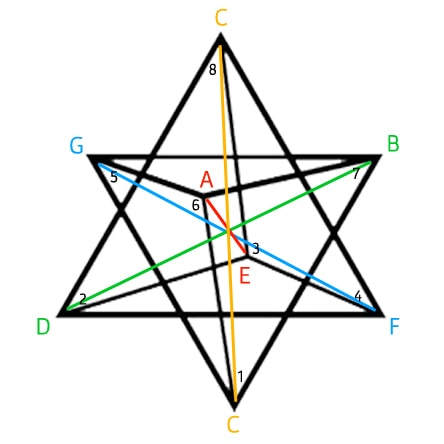
SEPTAGON

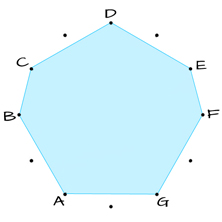
D – C – B – A – G – F – E – D

2 – 1 – 2 – 2 – 2 – 1 – 2

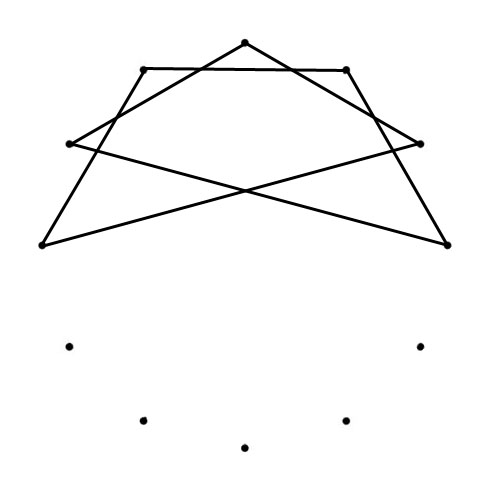
SEPTAGRAM

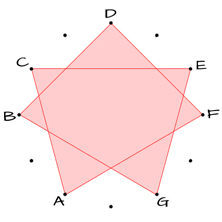
D – F – A – C – E – G – B – D

m3 – M3 – m3 – M3 – m3 – M3 – m3

SEPTAGRAM

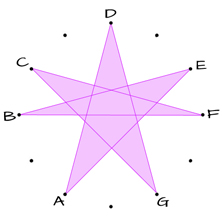
D – A – E – B – F – C – G – D

5th – 5th – 5th – TT – 5th – 5th – 5th

SUPERIMPOSED

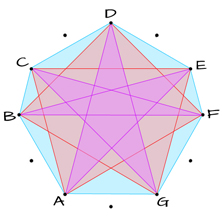
All tone connections.

When looking at this polygram now, you see how well “balanced” polygons and polygrams are formed with the Greek Modes.

The “Gemstone” Septagon connects the 7 tones using Minor and Major 2nds.
The red Septagram connects the 7 tones using Minor and Major 3rds.
The purple Septagram connects the 7 tones using 5ths and one Tritone (TT).

The “connected” tones in the images above, are the “white keys” on the piano.

The non-connected dots in the tone circles above – the “black keys” on the piano – form a pentagon and pentagram, the non-connected dots in the tone circles above – the “black keys” on the piano – form a pentagon and pentagram:

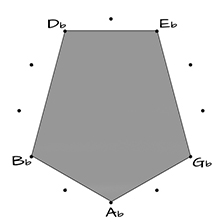
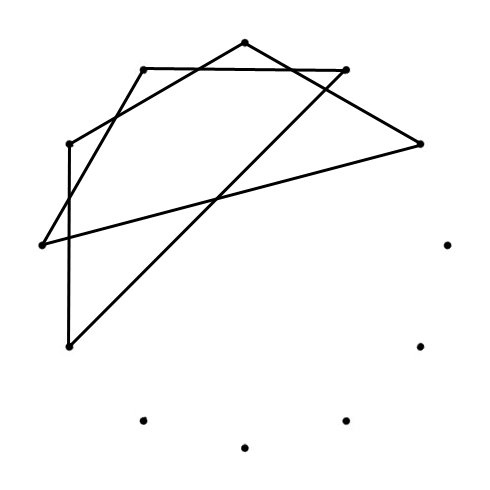
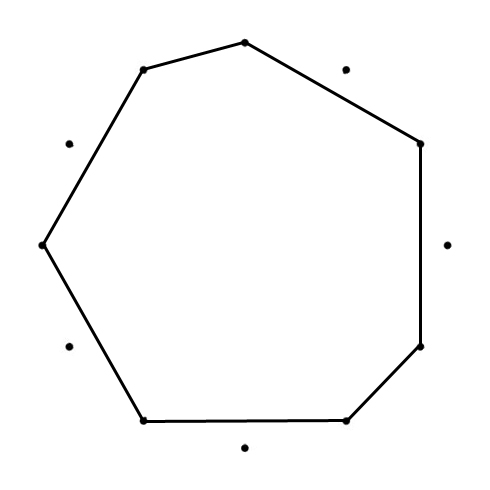
PENTAGON

Ab – Bb –Db – Eb – Gb – Ab

2 – m3 – 2– m3 – 2

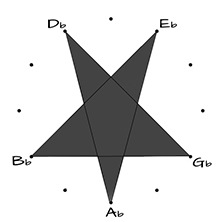
PENTAGRAM

Db – Ab – Eb – Bb – Gb – Db

4th <> 4th <> 5th > < 4th <> 4th

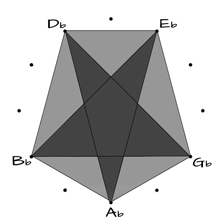
SUPERIMPOSED

White Keys (Greek Modes)
Black Keys (penta)

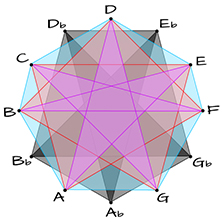
ALL SUPERIMPOSED

The pentagon connects the 5 tones using Major 2nds and Minor 3rds.
The pentagram connects the 5 tones using 4rds (descending) or 5ths (ascending).

The shape of the red polygon might look familiar to you:

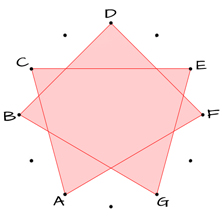
GEOMETRY OF SYMMETRICAL SCALES

In music, a symmetric scale is a music scale which equally divides the octave. The concept and term appears to have been introduced by Joseph Schillinger and further developed by Nicolas Slonimsky as part of his famous “Repository of Scales and Melodic Patterns“. In 12-tone equal temperament, the octave can only be equally divided into 2, 3, 4, 6 or 12 tone-spaces, which consequently may be filled in by adding the same exact interval or sequence of intervals to each resulting note (called “interpolation of notes”).

EQUALLY SPACED SCALES

CHROMATIC SCALE at CC

s–s–s–s–s–s–s–s–s–s–s

1-1-1-1-1-1-1-1-1-1-1

CHROMATIC SCALE at CoF

s–s–s–s–s–s–s–s–s–s–s

1-1-1-1-1-1-1-1-1-1-1

HEXATONiC SCALE at CC & CoF

T–T–T–T–T

2-2-2-2-2

MIRRORED SCALES

These 7-tone scales – when split in the middle – are mirrored on both sides of the center interval. Every first image bellow visualizes the Chromatic Circle (CC), every second the Circle of Fifths (CoF).

C NEOPOLITAN

s–T–T – T – T–T–s

1-2-2 – 2 – 2-2-1

C DORIAN

T–s–T – T – T–s–T

2-1-2 – 2 – 2-1-2

C MAJOR-MINOR

T–T–s – T – s–T–T

2-2-1 – 2 – 1-2-2

C DOUBLE HARMONIC

s–m3–s – T – s–m3–s

1-3-1 – 2 – 1-3-1

A few notes about the scales above:

The (modern) Dorian scale isn’t the only Greek mode with perfect symmetry (all Greek modes use the same shape polygon), but it’s “turned” so that the top of the “gemstone” polygon and the C on top of the Tone Circles align. The Dorian scale was traditionally the “1st mode” till the Ionian scale was added.
The “Major-Minor” scale (a Heptatonic scale) is actually the natural minor (Aeolian) scale but with a Major 3rd instead of a minor 3rd.
The Double Harmonic scale is also know as the “Arabic”, “Gypsy Major” or “Byzantine” scale. This scale contains a minor 2nd, major 3rd, perfect 4th and 5th, minor 6th, major 7th.

SCALES WITH REPEATING SEQUENCES

These scales – that “split” the octave in 2 – display the same sequence of intervals on both sides of the middle, except for the Augmented Scale that splits the octave in 3.

Every first image bellow visualizes the Chromatic Circle (CC), every second the Circle of Fifths (CoF).

C TRITONE

s–m3–T – s–m3–T

1-3-2 – 1-3-2

C 2-SEMITONE TRITONE

s–s–M3 – s–s–M3

1-1-4 – 1-1-4

C DIMINISHED *

T–s – T–s – T–s – T–s

2-1 – 2-1 – 2-1 – 2-1

C AUGMENTED *

m3–s – m3–s – m3–s

3-1 – 3-1 – 3-1

* The intervals of the Diminished and Augmented Scale pitch-pairs (2-1) and (3-1) can also be reversed: (1-2) and (1-3) to create the Auxiliary Diminished and Augmented Scales. The Polygons / Polygrams created will be the same, just turned 30 degrees clockwise.

A few notes about the scales above:

The Tritone scales are Hexatonic (6-tone) scales.

The Diminished and scale (also known as “Korsakovian” and “Pijper” scale) are Octatonic (8-tone) scales. The “Auxiliary” Diminished scale is the enharmonic equivalent of the “Petrushka Chord“.

The Augmented scale (used frequently by Jazz saxophonists such as John Coltrane, Oliver Nelson and Michael Brecker) is a Hexatonic scale containing an interlocking combination of two augmented triads a minor third apart.