HARMONICS, OVERTONES, FORMANTS, TIMBRE & SYMPATHETIC RESONANCE
A little information about harmonics, overtones, formants, timbre and sympathetic resonance and what effect a change of pitch might have on the way instruments and thus a music performance or recording sounds …
HARMONICS
The term harmonic has a precise meaning – that of an integer (whole number) multiple of the fundamental frequency of a vibrating object. The term overtone is used to refer to any resonant frequency above the fundamental frequency – an overtone may or may not be a harmonic. Harmonic overtones are the fundamental frequency multiplied, for example of the fundamental 216Hz: 432Hz (216 x 2), 648Hz (216 x 3), 864Hz (216 x 4), et cetera.
Besides the multiplications of the fundamental, there are other patters “embedded” within the harmonic series. The most clear is that of a sequence of doubling:
| Number sequence | Related Interval Names (within their relative Octaves) |
| 1-2-4-8-16-32-64-… | Tonic and it’s Octaves |
| When you proceed with listing these sequences … | |
| 3-6-12-24-48-… | Fifths (3 in relationship to 1, 6 in relationship to 2, et cetera) and Twelfths (6 in relationship to 1, 12 in relationship to 2, et cetera), et cetera. |
| 5-10-20-40-… | Major Thirds and Tenths |
| 7-14-28-56-… | Minor Sevenths |
| 9-18-36-72-… | Major Seconds and Ninths |
| 11-22-44-88-… | Tritones |
| 13-26-52-… | Minor Sixths |
| 15-30-… | Major Sevenths |
| 17-… | Minor Seconds and Flat Ninths |
| 19-… | Minor Thirds and Flat Tenths |
| 21-… | Augmented Thirds |
| 23-… | Supertritones |
| 25-… | Augmented Fifths |
| 27-.. | Major Sixths |
| 29-… | Neutral Sevenths |
| 31-… | Supermajor Sevenths |
| et ceterea. | |
… another sequence appears. Every doubling sequence within the harmonics series start with a following number of the odd numbers sequence: a(n) = 2*n + 1.
1-3-5-7-9-11-13-15-17-19-21-23-25-27-29-et cetera. https://oeis.org/A005408
With other words, a sequence (of the odd numbers), within a sequence (of doubling) within a sequence (multiplications) … pretty “cool”, isn’t it?
HOW DO HARMONICS FORM?
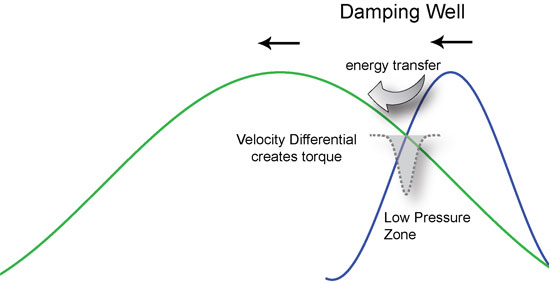
Source: Rick Merrick’s “Interference”
“As waves reflect and resonate inside a container or cavity, they cross one another. As they cross, they exchange energy at specific locations called ‘damping wells.’ In quantum mechanics this is explained by Landau-Zener theory (1932).
Known as Landau damping, waves that pass through one another mostly transparently, avoiding a direct collision, are called ‘avoided crossings.’ In such cases, energy is exchanged in a ‘parameter zone’ where one wave pushes against another, creating a kind of spinning well or vortex action. Like a kind of switch, energy is passed ‘adiabatically’ (without heat loss) across the damping well in a kind of torque action.
We can think of the damping well as a kind of low-pressure zone much like those in our atmosphere that create storms, hurricanes and tornados. The surrounding pressure differential causes an implosion toward the center of the low-pressure zone, forming a vortex.
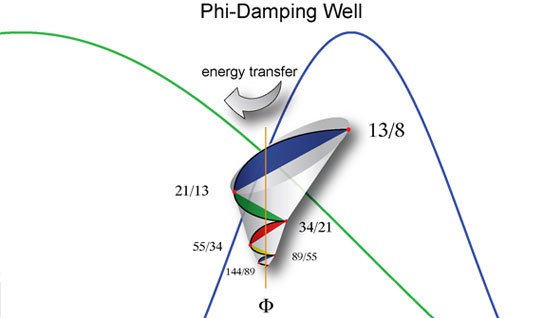
In the special case of a standing wave, damping wells form at constant locations at golden sections of the period of the prime resonant frequency. This is because the golden ratio constant, represented by the Greek letter Φ (or Phi) and equal to the ratio of about 1 : 0.618033… or 1.618033, is non-reflective while having the unique ability to nest into itself infinitely. As a result, energy is exchanged between harmonics at Phi proportions while harmonic wave partials begin to ripple outward from the edge of the well.
Because of this, the damping well of a standing waves can be described as a Fibonacci spiral converging to Phi, the deadest location in a standing wave and thus the point of greatest torque and energy exchange between harmonics. This can be proven by using the Fibonacci series as a nominal solution for the second-order equation known as the ‘characteristic wave damping equation.’ In this proof, the golden ratio Phi becomes the ‘eigenvector’ and the Fibonacci series (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …} become its ‘eigenvalues.’
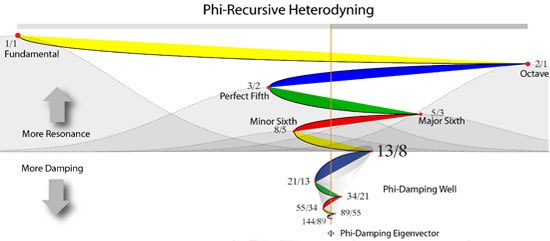
In fact, we can understand harmonic formation as something called ‘phi-heterodyning’ where each harmonic emerges around the Phi eigenvector in nested golden sections like a fractal. A paper by Bovenkamp and Giandinoto entitled ‘Incorporation of the Golden Ratio Phi into the Schrödinger Wave Function using the Phi Recursive Heterodyning Set’ shows how this can occur, but there is an easier way to visualize it.
The Fibonacci damping well approximates the irrational Phi Recursive Heterodyning Set with rational harmonic waves. Above the proportion of 13:8, wave formation is damped and suppressed while below this in the range of {1 .. 12} whole number harmonics can form and resonate constructively with the prime resonant frequency. In general, waves that come too close to Phi proportions in the resonant frequency are killed while those furthest away resonate the most.”
Note: In case you are interested in using the Fibonacci sequence for musical temperaments, then you might like to read the articles: “Fibonacci Temperaments” and “Fibonacci Tones“.
“While this sounds like a new idea, it is actually part of the age-old practice of creating resonant chambers that suppress the formation of unwanted standing waves and reflection. Stradivarius was well-known for using golden sections in the design of his violins. The best rectangular concert halls use golden proportions in their dimensions, as do modern day speaker enclosures.“
— end text written by Rick Merrick
OVERTONES
An “overtone” is any frequency higher than the fundamental frequency of a sound. “Harmonic overtones” are the fundamental frequency multiplied. The fundamental and the overtones together are called partials (a “partial wave” or “constituent frequency”).
Note: the 1st overtone is the 2nd harmonic.
PITCH, OVERTONES AND HUMAN HEARING
The human hearing range is commonly given as 20 to 20,000Hz. Under ideal laboratory conditions, humans can hear sound as low as 12 Hz. Some children are capable of hearing frequencies above 20,000Hz but with age this range will shrink usually beginning at around age of eight with the upper frequency limit being reduced.
Low tones can potentially produce more overtones within our hearing range then high tones can. It is important to understand that their is theoretically no limit to the number of potential overtones that can be generated. That we practically detect less overtones created by a piccolo Trumpet then by a Tuba is not because a piccolo produces less overtones, but many of it’s overtones might overshoot the high end boundary of our hearing.
So, to visualize the difference between two tones of different pitch I will calculate the number of the first overtone that overshoots 20,000Hz, starting with the 1st Harmonic (the “fundamental”) of the tones A3 and A4 in the example table below:
| 1 | 2 | 3 | 5 | 10 | 20 | 40 | 47 | 80 | 92 |
| 216Hz | 432 | 648 | 1,080 | 2,160 | 4,320 | 8,640 | 10,152 | 17,280 | 20,088 |
| 432Hz | 864 | 1296 | 2,160 | 4,320 | 8,640 | 17,280 | 20,304 | 34,560 | 39,744 |
What we see in this table is that if we use 216Hz as fundamental, this tone could generate 92 overtones before we overshoot the 20,000Hz, but if we use 432Hz as fundamental, this tone could generate only 47 overtones before we overshoot the 20,000Hz.
NOTE: You could do the same with any other frequency, A3=220Hz and A4=440Hz would generate a similar progression and relative difference in harmonics.
INSTRUMENTS, HARMONICS, FORMANTS AND TIMBRE
Many of the instruments, those utilizing strings or air columns, produce the fundamental frequency and harmonics. Their overtones can be said to be harmonic. Other sound sources such as the membranes or other percussive sources may have resonant frequencies which are not whole number multiples of their fundamental frequencies. They are said to have non-harmonic / inharmonic overtones. Some musical instruments could produce overtones that are slightly sharper or flatter than true harmonics. The sharpness or flatness of the overtones is one of the elements that contributes to their unique sound (timbre). This also has the effect of making their wave forms not perfectly periodic. Sympathetic resonance could play a role in this.
With other words: The timbre of an instrument is determined by which overtones it emphasizes. That is to say, the relative volumes of these overtones to each other determines the specific “flavor” or “color” of sound of that family of instruments.
When we see a spike of energy in a harmonic is because the resonator (in this case an instrument) has aligned its value or formant to that harmonic. The Acoustical Society of America (ASA) defines a formant as: “a range of frequencies in which there is an absolute or relative maximum in the sound spectrum”. A smaller instrument has a higher formant value, which aligns with higher harmonics. A larger instrument has a lower formant value, so it brings out the lower harmonics. A musical instrument may have several formant regions due to the shape and resonance properties of the instrument. The human voice also has formant regions determined by the size and shape of the nasal, oral and pharyngeal cavities (i.e. the vocal tract), which permit the production of different vowels and voiced consonants.
With other words, every type of instrument has it’s own unique sound due to formants – a combination (set) of overtones – that are generated by the particular instrument in relationship to the range(s) of formants related to the “design” of the instrument. The formants generated for example with a saxophone is a different “selection” from the harmonic series then the formants generated by for example a guitar.
Bo Constantinsen (whatmusicreallyis.com) made short example video:
SYMPATHETIC RESONANCE
The resonance vibrations of the natural frequencies of the material an instrument is made of could trigger sympathetic vibrations and with it alter the loudness of certain overtones generated within the instrument. Sympathetic resonance or sympathetic vibration is a harmonic phenomenon wherein a formerly passive string or vibratory body (resonator) responds to external vibrations to which it has a harmonic likeness. When an instrument is “forced” to resonate at one or more of its natural frequencies, it vibrates in such a way that a standing wave is formed within the instrument. The natural frequencies of an instrument are the harmonic frequencies at which standing wave patterns are established within the instrument. The specific resonance frequency could “support” particular overtones from the “set of overtones” within the formant range that are characteristic to the instrument type.
It might be possible that due to the change of pitch some natural frequencies trigger different sympathetic resonances then before the pitch change, a shift or re-balance of sympathetic resonance within the formant range(s) of the instrument.
An instrument should not suddenly generate “additional” frequencies (outside the “set”) because of a pitch change. Additional frequencies might be the result of “mechanical issues” (like interference, antiresonance, et cetara) of the instrument, but a change of pitch would normally not generate “additional” overtones under normal conditions and with a proper build instrument.
CHANGE OF PITCH = CHANGE (SHIFT) OF LOUDNESS OF PARTICULAR HARMONICS
Formant regions are not directly related to the pitch of the fundamental frequency of a generated tone and may remain more or less constant as the fundamental changes. If the fundamental is well below or low in the formant range of the particular instrument, then the quality of the sound is rich, but if the fundamental is above the formant region(s) the sound is thin.
This is why the sound of an instrument might sound a bit “warmer” when we change the pitch from 440Hz to 432Hz. The lower pitch does not change the “set” or overtones or the range of formants, but might emphasize different (in this case lower) harmonics within the formant range(s).
POST PRODUCTION RE-PITCHING & OVERTONES
Changing the pitch of recorded material will NOT change / re-balance the harmonics of the instruments used for the recording. The number of overtones will NOT change when re-pitching recorded material! The only thing that might change by re-pitching recorded material is the way the sound ‘interacts’ within the space were the music is played.
Post production re-pitching (like any other “manipulation” of the original recorded material) could cause loss of sound quality. This is most obvious with the higher frequencies (“high end”), in particular when only Pitch but not Tempo is changed (or visa versa). Only when both pitch and tempo are changed during post-production re-pitching, only then the loss of sound quality is “negligible”.
More information on how to change the concert pitch in post production …
REFERENCES:
- “Interference” by Rick Merrick
- http://en.wikipedia.org/wiki/Harmonic_series_(music)
- http://en.wikipedia.org/wiki/Overtone
- http://en.wikipedia.org/wiki/Formant
- http://www.sengpielaudio.com/calculator-harmonics.htm
- http://en.wikibooks.org/wiki/Physics_Study_Guide/Wave_overtones
- http://hyperphysics.phy-astr.gsu.edu/%E2%80%8Chbase/sound/soucon.html

